Homeomorphism (graph theory)

Not to be confused with graph homomorphism.

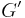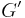In graph theory, two graphs $G$ and $G'$ are homeomorphic if there is an isomorphism from some subdivision of $G$ to some subdivision of $G'$ . If the edges of a graph are thought of as lines drawn from one vertex to another (as they are usually depicted in illustrations), then two graphs are homeomorphic to each other in the graph-theoretic sense precisely if they are homeomorphic in the sense in which the term is used in topology.

1 Subdivisions
- 1.1 Barycentric Subdivisions
2 Embedding on a surface
3 Example
4 See also
5 References

Subdivisions

In general, a subdivision of a graph G is a graph resulting from the subdivision of edges in G. The subdivision of some edge e with endpoints {u,v} yields a graph containing one new vertex w, and with an edge set replacing e by two new edges, {u,w} and {w,v}.

For example, the edge e, with endpoints {u,v}:

can be subdivided into two edges, e₁ and e₂, connecting to a new vertex w:

The reverse operation, smoothing out or smoothing a vertex w with regards to the pair of edges (e,f) incident on w, removes both edges containing w and replaces (e,f) with a new edge that connects the other endpoints of the pair. Here it is emphasized that only 2-valent vertices can be smoothed.

For example, the simple connected graph with two edges, e₁ {u,w} and e₂ {w,v}:

has a vertex (namely w) that can be smoothed away, resulting in::

Determining whether for graphs G and H, H is homeomorphic to a subgraph of G, is an NP-complete problem.

Barycentric Subdivisions

The barycentric subdivision subdivides each edge of the graph. This is a special subdivision, as it always results in a bipartite graph. This procedure can be repeated, so that the n^th barycentric subdivision is the barycentric subdivision of the n-1^th barycentric subdivision of the graph. The second such subdivision is always a simple graph.

Embedding on a surface

It is evident that subdividing a graph preserves planarity. Kuratowski's theorem states that

a finite graph is planar if and only if it contains no subgraph homeomorphic to K₅ (complete graph on five vertices) or K_3,3 (complete bipartite graph on six vertices, three of which connect to each of the other three).

In fact, a graph homeomorphic to K₅ or K_3,3 is called a Kuratowski subgraph.

A generalization, flowing from the Robertson–Seymour theorem, asserts that for each integer g, there is a finite obstruction set of graphs 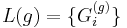$L(g) = \{G_{i}^{(g)}\}$ such that a graph H is embeddable on a surface of genus g if and only if H contains no homeomorphic copy of any of the 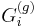$G_{i}^{(g)}$ . For example, 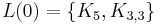$L(0) = \{K_{5}, K_{3,3}\}$ contains the Kuratowski subgraphs.

Example

In the following example, graph G and graph H are homeomorphic.

If G' is the graph created by subdivision of the outer edges of G and H' is the graph created by subdivision of the inner edge of H, then G' and H' have a similar graph drawing:

G', H'

Therefore, there exists an isomorphism between G' and H', meaning G and H are homeomorphic.

References

Yellen, Jay; Gross, Jonathan L. (2005), Graph Theory and Its Applications, Discrete Mathematics and Its Applications (2nd ed.), Boca Raton: Chapman & Hall/CRC, ISBN 978-1-58488-505-4